机器学习笔记

发表于 |

吴恩达老师《Machine Learning》课程的学习笔记

简介

机器学习算法

Tom Mitchell provides a more modern definition: “A computer program is said to learn from experience E with respect to some class of tasks T and performance measure P, if its performance at tasks in T, as measured by P, improves with experience E.”

有监督学习

在有监督学习中，我们有数据集并且有相对应的正确输出，知道输入和输出之间存在着某种关系。

  • 回归(regression)：例如给出一张照片，预测照片中人物的年龄
  • 分类(classification)：例如判断一个病人的肿瘤是良性还是恶性

无监督学习

无监督学习中，我们可以解决那些并不知道结果是怎样的问题。我们可以获得数据的结构，即便我们并不知道各变量的影响。

基于数据中变量间的关系对数据进行聚类(clustering)，我们可以获得数据的结构。

无监督学习中，预测的结果是没有反馈的。

其他

reinforcement learning, recommender system。

单变量线性回归(Linear Regression with One Variable)

模型和费用函数

模型表示

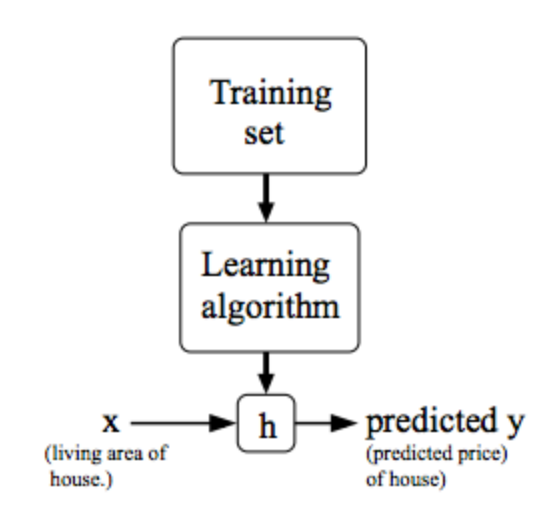
比如h函数可以是$h_\theta(x)=\theta_0+\theta_1 x$

这样的就是单变量线性回归(linear regression with one variable/univariate linear regression)

符号：

x表示房子大小

y表示房价

m表示训练集样本数

h函数，是一个从x到y的映射

$x^{(i)}$表示的是训练集中第i个x的值，i用于表示索引，$y^{(i)}$同理

费用函数

Hypothesis: $h_\theta(x) = \theta_0+\theta_1x$

有了这样的假设之后，一个重要的问题是：如何选择参数$\theta$的值？

既然我们要用这个假设进行预测，那么就要恰当选择参数的值使得模型尽可能准确。思想是这样的：选择$\theta0,\theta_1$的值，使得$h\theta(x)$靠近训练集的y值。

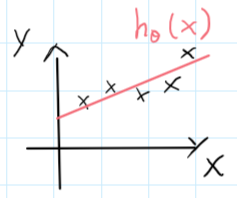
（上图，黑色叉表示训练集样本，我们要找到这样一条直线，即选择参数，使得这条直线尽可能拟合这些点）

引入费用函数

Squared Error Function

我们所要做的，就是选择参数$\theta$使得J函数尽可能小

关于费用函数的直觉

Hypothesis: $\quad h_\theta(x)=\theta_0+\theta_1x$

Parameters: $\quad \theta_0, \theta_1$

Cost Function: $J(\theta0,\theta_1) \frac{1}{2m} \displaystyle \sum{i=1}^m (h_\theta(x^{(i)})-y^{(i)})$

Goal: $\qquad \qquad \min_{\theta_0,\theta_1} \space J(\theta_0,\theta_1)$

画出J函数关于参数$\theta$的图像如下

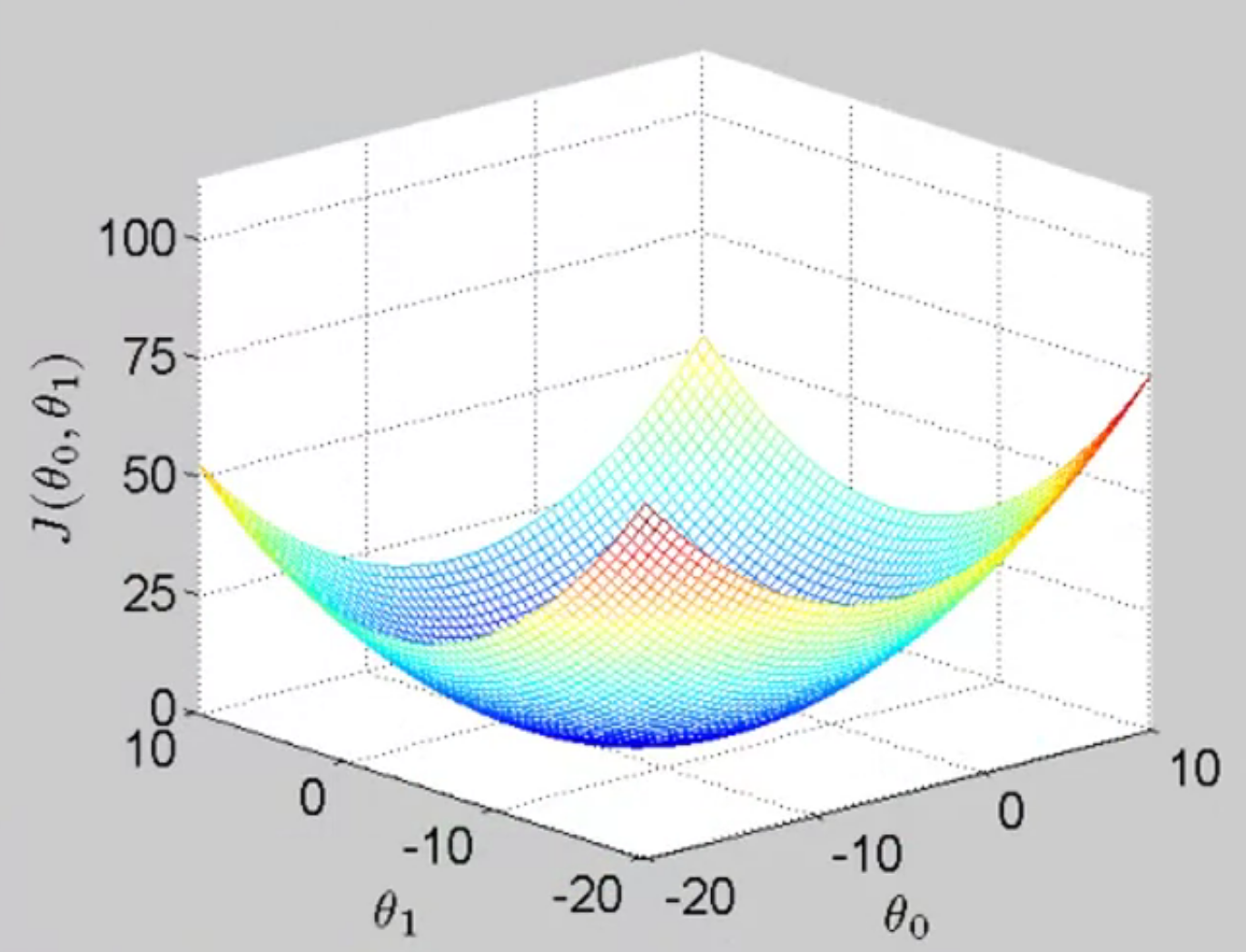
参数学习

梯度下降

框架：

  • 从某些参数$\theta$开始
  • 不断改变参数的值来缩小目标函数的值，直到最后到达一个最小值

具体：

不断重复如下步骤直到收敛：

$\alpha$在这里称为learning rate，$\alpha$越大下降越快。

注意：参数$\theta$是同时更新的(simultaneous update)

learning rate太小：梯度下降会比较慢

learning rate太大，可能会无法收敛

learning rate不用经常改变，对于固定的learning rate，梯度下降方法是可以收敛到局部最优的

若已经处在局部最优点，梯度下降会停在这里，因为这一点梯度值为0

线性回归问题的梯度下降方法

线性回归问题的费用函数是凸函数，局部最优解即是全局最优解

“Batch Gradient Descent”

Batch：每一步梯度下降都使用所有的训练样本

多变量线性回归(Linear Regression with Multiple Variable)

多变量线性回归

多特征

符号：

$x_j^{(i)}$：第i个训练样本的第j个特征

$x^{(i)}$：第i个训练样本输入（包含所有特征）

m：训练样本总数

n：特征总数

Hypothesis：

令$x_0=1$，可以写成如下形式

多变量的梯度下降

实践中的梯度下降——特征缩放

思想：令特征都在一个相似的数值范围中

使得每一个特征都差不多位于范围$-1 \leq x_i \leq 1$

均值归一化

将$x_i$替换乘$x_i-\mu_i$使得特征都大致接近均值（不对$x_0$应用）

其中$\mu_i$是特征i的平均值，$s_i$是取值的范围（max-min），或者是标准差(standard deviation)

实践中的梯度下降——学习速率

怎么样选择一个好的学习速率$\alpha$呢？——>画图看

看minJ函数的值，如果运行正确，函数图像值应随迭代次数的增加而下降

如果图像出现了以下异常，那么应该选择一个更小的$\alpha$值

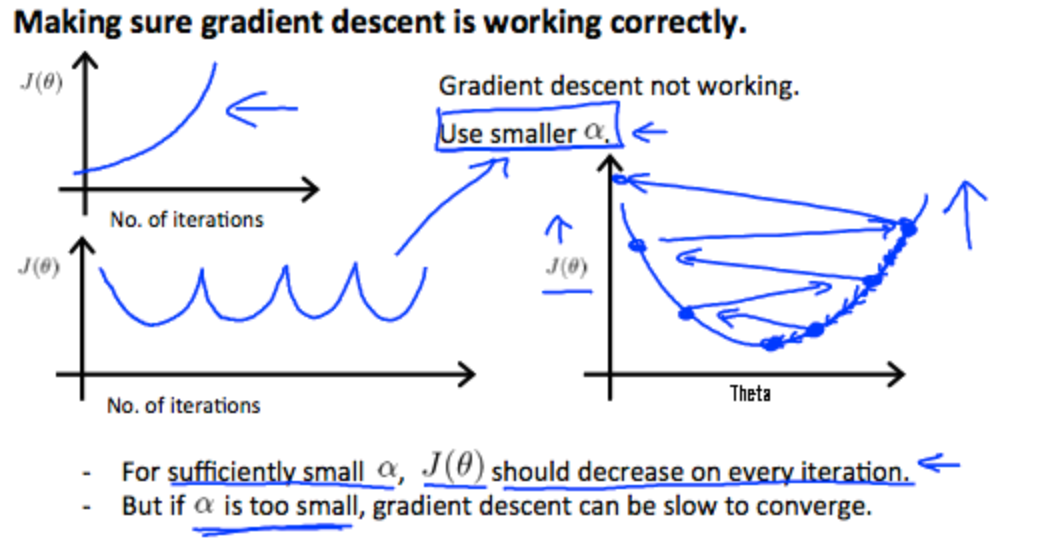
选择$\alpha$的值：尝试…,0.001,0.003,0.01,0.03,0.1,0.3,1,…之类的，看看图像的走向和下降速度，确定一个较好的范围

特征和多项式回归

hypothesis function并不一定要是线性的（直线），我们可以有二次的，三次的，或者是平方根的项。比如$h_\theta(x) = \theta_0 + \theta_1x^2+\theta_2x^3$

多项式的假设可以通过添加特征的方式，来转换成线性回归的形式

比如说$x^2$记为特征$x_1$，$x^3$记为特征$x_2$

用解析的方法计算参数

Normal Equation

（注意仅适用于线性回归问题）

直觉：在1D的情况下，目标函数$J(\theta) = a\theta^2 + b\theta +c$，这是一个二次函数。我们都知道怎么通过解析的方式，直接求得它的最小值。

类似地，对于其他维数，线性回归问题的J函数最小值是有解析解的。

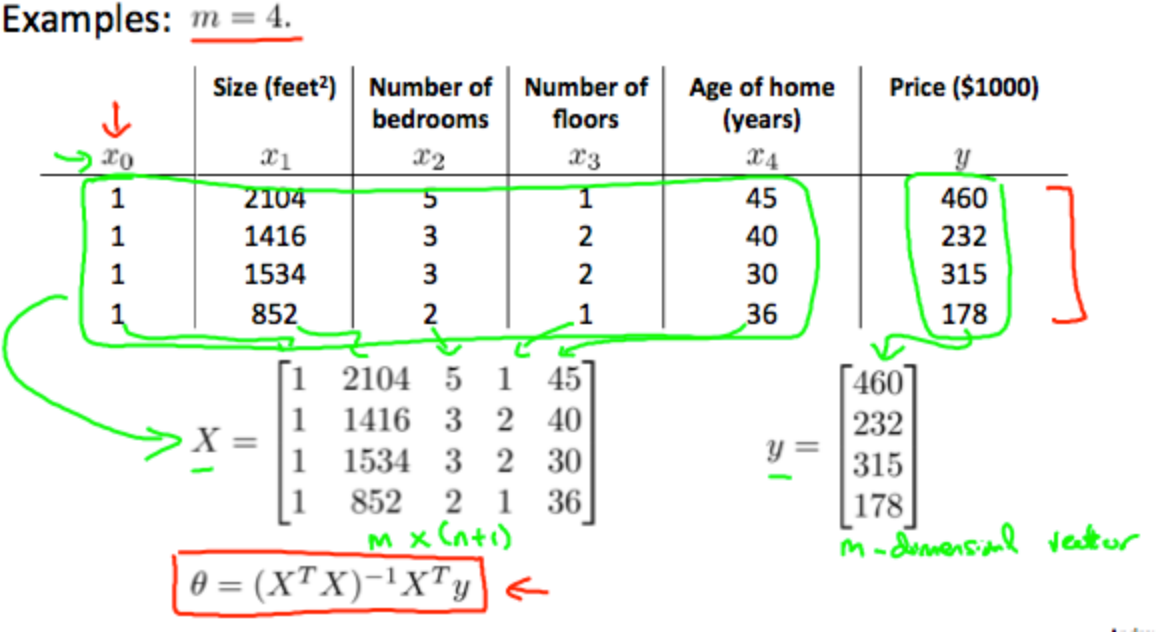
求得这个解析解的方法是对每一个参数$\theta$求偏导，然后使得这些偏导为0，求出$\theta$值。在这里不进行推导。结果如下：

其中X矩阵(design matrix)和y向量如下：

梯度下降和Normal Equation对比

梯度下降 Normal Equation
要选择$\alpha$ 不必选择$\alpha$
要迭代很多次 不必迭代很多次
当特征很多（n很大）时，表现良好，$O(kn^2)$ 要计算$(X^TX)^{-1},O(n^3)$
一般$n \geq 10^6$选择这个 当n很大时很慢

使用Normal Equation时，当$X^TX$不可逆怎么办？

Octave: pinv()函数

  • 冗余特征（线性依赖）
    • 如$x_1$是以平方米为单位的面积，$x_2$是以平方英尺为单位的面积
  • 太多特征（如$m \leq n)$
    • 删掉一些特征，或者使用正则化

编程作业1 Linear Regression

(待补充)

Logistic Regression

分类和表示

分类

Main idea：用线性回归解决分类问题不是一个好的方案

在分类问题中，y值为0或1（二元分类），但是线性回归的函数值可以大于1或小于0

Logistic Regression $0 \leq h_\theta(x) \leq 1$

这个是用来解决分类问题的

假设表示

g函数称为sigmoid fucntion/logistic function

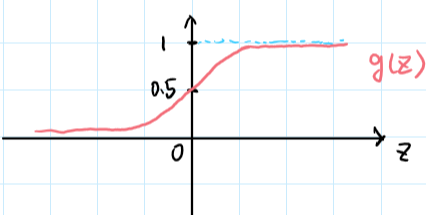
$h_\theta(x)$评估在输入为x的情况下，y=1的可能性

决策边界

线性的决策边界

若我们有$h_\theta(x) = g(\theta^Tx)$，其中$g(z) = \frac{1}{1+e^{-z}}$

假设若$h\theta(x) \geq 0.5$，我们预测$y = 1$，若$h\theta(x) < 0.5$，我们预测$y = 0$

而根据$g$函数的图像，我们可以知道当$z \geq 0$时，$g(z) \geq 0.5$，即对于，当$\theta^Tx \geq 0$时，$h_\theta(x) \geq0.5$

因此决策边界为直线$\theta^Tx = 0$

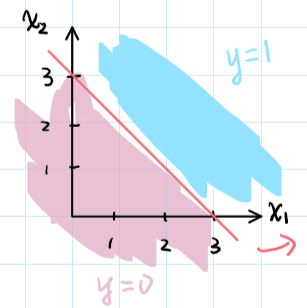
若$h_\theta(x) = g(\theta_0 + \theta_1x_1 \theta_2 x_2)$，其中$\theta = [-3;1;1]$

则有当$\theta_0 + \theta_1x_1 \theta_2 x_2 \geq 0$时有$y = 1$，因此我们可以画出决策边界$-3 + x_1 + x_2 \geq 0$

非线性的决策边界(non-linear decision boundaries)

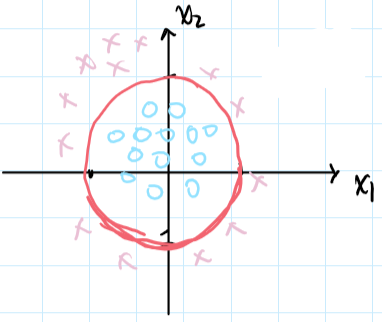
假设$h_\theta(x)=g(\theta_0 + \theta_1 x_1 + \theta_2 x_2 + \theta_3 x_1^2 + \theta_4 x_2^2),\quad \theta = [-1;0;0;1;1]$

将$\theta$的值代入，则有当$-1 + x_1^2 + x_2^2 \geq 0$时，我们预测$y = 1$，得到的决策边界如下

Logistic Regression Model

Cost Function

训练集：${(x^{(1)},y^{(1)}),(x^{(2)},y^{(2)}),…,(x^{(m)},y^{(m)})}$一共m个样本

其中$x = [x_0;x_1;…;x_n]\in R^{n+1},\space x_0 = 1,\space y \in {0,1}$

$h_\theta(x) = \displaystyle \frac{1}{1+e^{-\theta^Tx}}$

若直接把$h_\theta(x)$代入线性回归的费用函数中，得到的费用函数是非凸的。因此，logistic regression的cost定义如下：

图像如下：

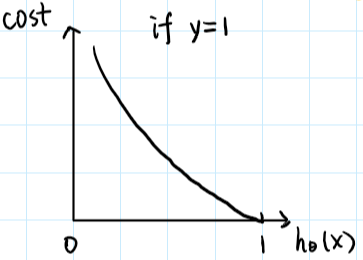
我们可以看到，当y=1，且$h\theta(x) = 1$时，$cost = 0$；但是当$h\theta(x) \rightarrow 0$时$cost \rightarrow \infin$

一种直觉的解释：若病人有坏肿瘤（y=1），而预测结果为良性（$h_\theta(x) \rightarrow 0$)，那么代价就趋向$\infin$

Simplified Cost Function and Gradient Descent

我们把所有样本的cost加起来并平均，就得到了J函数

对于一个logistic regression的问题，我们的目标就是要寻找使得$J$函数值最小的参数$\theta: min_\theta J(\theta)$

梯度下降

$J(\theta) = \displaystyle -\frac{1}{m}[\sum{i=1}^my^{(i)}logh\theta(x^{(i)})+(1-y^{(i)})log(1-h_\theta(x^{(i)})) ]$

要确保梯度下降是正确运行的，我们可以绘制$J(\theta)$和迭代次数$(#iterations)$之间的关系的图像

logistic regression可应用Feature Scaling

Advanced Optimization

给定$\theta$，我们需要写出计算如下两项的代码：

  • $J(\theta)$
  • $\displaystyle \frac{\partial}{\partial \theta_j} J(\theta) \space (for\space j = 0,1,…n)$

优化算法：

  • 梯度下降
  • conjufate gradient
  • BFGS
  • L-BFGS

优点：

  • 不需要人为选择$\alpha$
  • 通常比梯度下降要快

缺点：

  • 更为复杂

Multiclass classification

多分类问题。解决方案：one-vs-all

举个例子。比如说我们要进行天气的预测，预测结果可能有sunny, cold, raniny，使用one-vs-all的方法，对每一类都使用一个logistic regression hypothesis，把多分类的问题转换为多次二分类的问题。如下：

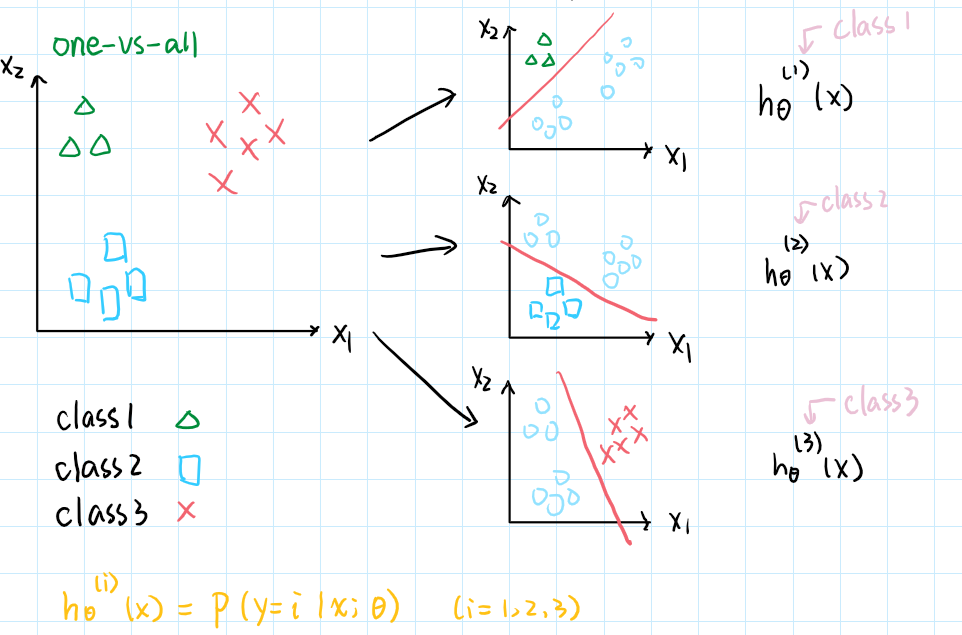
对每一类都训练一个回归分类器，用来预测这一类。

对于一个新的样本，把它归到预测值最高的那一类

正则化(Regularization)

解决过度拟合的问题(solving the problem of overfitting)

过度拟合的问题

举个例子，房价预测的线性回归模型

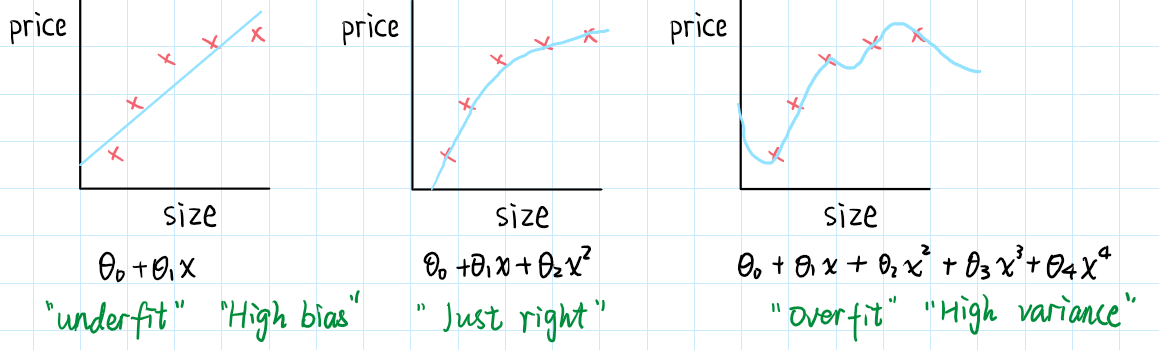
过度拟合： 如果我们有太多的特征，经过学习之后模型能够很好地拟合训练集的数据($J(\theta) \approx 0$)，但是这个模型在预测新样本上表现并不好。

校正过度拟合

可选项如下：

  1. 减少特征的数量
    • 人工选择哪些特征是需要保留的
    • 模型选择算法（稍后讨论）
  2. 正则化
    • 保留所有的特征，但是减少$\theta_j$的值/高度
    • 当我们拥有很多特征时表现较好，每一个特征在预测y上都有一点贡献

费用函数

正则化：较小的参数值$\theta_0,\theta_1,…\theta_n$

  • 更“简单”的假设
  • 更少可能产生过度拟合

当$\lambda$太大的时候的问题：$\thetaj \approx 0(j \geq 1), h\theta(x) = \theta_0$，就会underfit

正则化的线性回归

费用函数

梯度下降

在上述式子中，$\theta_j$也可以写成

编程作业2: Logistic Regression

1 Logistic Regression

建立模型，预测一个学生是否会被录取

首先是画图：X是m*2特征矩阵，y是录取结果

plotData.m

1
2
3
4
5
6
7
8
function plotData(X, y)
    figure; hold on;
    pos = find(y == 1);
    neg = find(y == 0);
    plot(X(pos,1),X(pos,2),'k+','LineWidth',2,'MarkerSize',7);
    plot(X(neg,1),X(neg,2),'ko','MarkerFaceColor','y','MarkerSize',7);
    hold off;
end

接下来是实现sigmoid函数，主要注意z可能是向量或矩阵，因此要用element wise操作符

sigmoid.m

1
2
3
4
function g = sigmoid(z)
    g = zeros(size(z));
    g = 1 ./ (1 + e .^ (-z));
end

计算费用函数J和梯度，这里用的是矩阵乘法，把X当成整个矩阵计算：

costFunction.m

1
2
3
4
5
6
7
8
9
10
11
12
function [J, grad] = costFunction(theta, X, y)
	m = length(y); 
	J = 0;
    grad = zeros(size(theta));
	%计算J
    summation = -y' * log(sigmoid(X*theta))-(1-y)'*log(1-sigmoid(X*theta));
    J = summation / m;
	%计算梯度
    prediction = sigmoid(X*theta);
    error = prediction - y;
    grad = 1/m * (X'*error);
end

note: 梯度维数是(n+1)*1的，因此最后直接是X的转置乘上error就ok了，（自己纠结过一下，搞错了梯度是一维的，加起来就错了）

使用fminunc函数计算参数

1
2
3
options = optimset('GradObj', 'on', 'MaxIter', 400);
[theta, cost] = ...
	fminunc(@(t)(costFunction(t, X, y)), initial_theta, options);

根据算得的theta和给定的X进行预测：大于0.5的返回1

predict.m

1
2
3
4
5
6
7
function p = predict(theta, X)
	m = size(X, 1)；
	p = zeros(m, 1);
    hypothesis = sigmoid(X*theta);
    pos = find(hypothesis >= 0.5);
    p(pos) = 1;
end

2 Regularized logistic regression

实现一个正则化的logistic regression模型，预测工厂产的芯片是否能通过QA

可视化部分和前面类似。

mapFeature.m 做的工作是将x1，x2的多项式乘积映射成新的特征

然后是费用函数和梯度的计算。费用函数多了正则化的一项。梯度计算的时候，要注意对theta0求偏导的项和其他项不太一样，少了正则化的部分。

costFunctionReg.m

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
function [J, grad] = costFunctionReg(theta, X, y, lambda)
    m = length(y); % number of training examples
    J = 0;
    grad = zeros(size(theta));
	%计算费用函数J
    summation = sum(-y.*log(sigmoid(X*theta))-(1-y).*log(1-sigmoid(X*theta)));
    term1 = summation / m;
    theta_square = theta .^2;
    theta_square(1,:) = []; %delete the first row of theta
    term2 = lambda/(2*m) * sum(theta_square);
    J = term1 + term2;
	%计算梯度
    hypothesis = sigmoid(X*theta);
    error = hypothesis - y;
    term1 = 1/m * (X'*error);
    term2 = lambda/m * theta;
    term2(1) = 0;
    grad = term1 + term2;

end

神经网络：表示(Neural Networks: Representation)

编程作业3 Multi-class Classification and Neural Networks

实现 one-vs-all logistic regression和神经网络识别手写数字。

Multi-class Classification

一个图片是2020像素的，一个图片展开成一个400维的向量，总共有5000个样本。数据集是5000\400大小的矩阵X。另有一个5000维的矩阵y，标记了每一个样本表示的数字。数字0的标记为10，1-9数字的标记对应为1-9

可视化数据

随机抽取X矩阵的其中100行，作为参数传递到displayData函数中。此函数将矩阵的一行变为20*20的灰度图像，并将所有的图像一起展示出来。（关注如何实现，imagesc函数和display_array）

向量化实现

编程作业2中已经是向量化的实现了。可直接用。

one-vs-all分类

对每一个类别都进行计算，得到theta，用的是fmincg函数，注意调用函数的方法。把每一个类别的theta都整合到一起，形成一个矩阵num_labels*(n+1)大小的矩阵。

oneVsAll.m

1
2
3
4
5
6
7
8
9
10
11
12
13
14
function [all_theta] = oneVsAll(X, y, num_labels, lambda)
    m = size(X, 1);
    n = size(X, 2);
    all_theta = zeros(num_labels, n + 1);
    X = [ones(m, 1) X];
    initial_theta = zeros(n + 1, 1);
    options = optimset('GradObj','on','MaxIter',50);
    %使用循环，对每一个类别都进行训练
    for c = 1 : num_labels,
        [theta] = fmincg(@(t)(lrCostFunction(t, X, (y==c), lambda)),initial_theta,options);
        theta = theta(:)'; %确保theta变成了行向量
        all_theta(c,:) = theta;
    end
end

接下来根据算得的all_theta，可以进行预测。

predicOneVsAll.m

1
2
3
4
5
6
7
8
9
function p = predictOneVsAll(all_theta, X)
    m = size(X, 1);
    num_labels = size(all_theta, 1);
    p = zeros(size(X, 1), 1);
    X = [ones(m, 1) X];
    predict = X * all_theta';
    %find the maximun index of each row
    [w, p] = max(predict, [], 2); %注意max函数的用法，找到每一行的最大值及对应索引
end

Nueral Networks

给定了算好的theta值，三层的神经网络，进行预测。

1
2
3
4
5
6
7
8
9
10
11
12
13
function p = predict(Theta1, Theta2, X)
    m = size(X, 1);
    num_labels = size(Theta2, 1);
    p = zeros(size(X, 1), 1);
    X = [ones(m,1) X];
    z2 = X * Theta1';
    a2 = sigmoid(z2);
    a2 = [ones(m,1) a2]; %add bias unit	
    z3 = a2 * Theta2';
    hypothesis = sigmoid(z3);
    [w idx] = max(hypothesis,[],2);
    p = idx;
end

神经网络：学习(Neural Networks: Learning)

编程作业4 Neural Networks Learning

实现神经网络backpropagation算法，并应用到手写数字识别中。

这次编程作业感觉要难不少，特别是backprop部分（主要一个是因为之前课程录像中ppt有关于正则化的梯度公式有错误，整了半天backprop是ok的但带正则化总是过不了。另一个则是在sigmoidGradient函数调用处，正确用法是sigmoidGradient(z2)或者a2.*(1-a2)，在de正则化梯度的bug时候脑子一热把a2作为参数传进函数了…后面发现之后才改过来【汗】），在bug de不出来的时候看看课程论坛总是好的，很快就发现自己的问题所在了。

Neural Networks

数据和前一次编程练习中一样，可视化过程也一样。

实现神经网络的费用函数和梯度计算

费用函数

首先实现不带正则化的费用函数，到计算hypothesis之前的步骤都是上次实验实现过的，拿过来用就可。例如，hypothesis的第二行第一列表示的是第二个样本属于第一类的可能性，第二行第三列表示第二个样本属于第三类的可能性。hypothesis矩阵大小为m*k。

根据费用函数的公式，我们知道，要对每一个样例的每一个类别都进行误差的计算。注意到，我们读入的y是一个列向量m1。也就是说y直接标示了每一个样本是哪一个类别的。为了方便计算，我们将y改写一下，变成m\k大小，把它变成一个0/1矩阵来标示类别。比如原来y的第一行是10，新的Y矩阵中第一行中只有第10列为1，其他的全为0。这样来表示第一个样本属于类别10。

这样一来，新的矩阵Y的每一行每一列对应的就是每一个样本的每一类。hypothesis的也是这样。再回看费用函数，要对每一个样本的每一类，计算hypothesis和y之间的误差。利用新矩阵Y和hypothesis矩阵，可以通过点乘的方式将对应样本的对应类别分别进行计算。最后，再将矩阵中所有元素都加起来，就是费用函数中连续两个求和部分的结果了。

实现完这部分之后，运行ex4验证一下计算结果，与预期的一致。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
m = size(X, 1);
J = 0;
Theta1_grad = zeros(size(Theta1));
Theta2_grad = zeros(size(Theta2));

X = [ones(m,1) X];
z2 = X * Theta1';
a2 = sigmoid(z2);
a2 = [ones(m,1) a2]; %add bias unit	
z3 = a2 * Theta2';
hypothesis = sigmoid(z3);
% use the Feedforward method to compute hypothesis
% hypothesis 是一个m*k的矩阵。一行对应一个样例，一列对应一个类别。

% extend y into a matrix whick size is m*K
Y = zeros(m,num_labels);
for i = 1 : m,
    Y(i,y(i)) = 1;
end
term1 =-1/m * sum(sum(Y.*log(hypothesis)+(1-Y).*log(1-hypothesis)));
J = term1;

（转换y到Y矩阵的时候我用的是for循环，感觉还是太拖沓了，或许还有更简洁的实现方法？）

那么下一步就可以顺带实现费用函数的正则化部分了。正则化部分的内容相对简单一些，就是将神经网络中的Theta矩阵中除去与bias unit相关的部分，其他元素进行平方，然后全部加起来即可。要注意的一点是Theta矩阵中和bias unit相关的位置。我在实现feedForward的时候，加bias unit时是放在了最前面的。因此，Theta矩阵中对应bias unit部分的就是第一列，把第一列置0就好，也方便后面正则化梯度用。

1
2
3
4
5
6
7
% bias unit relates to column 1
noBiasTheta1 = Theta1;
noBiasTheta1(:,1) = zeros(size(Theta1,1),1);
noBiasTheta2 = Theta2;
noBiasTheta2(:,1) = zeros(size(Theta2,1),1);
term2 = lambda/(2*m) * (sum(sum(noBiasTheta1.^ 2)) + sum(sum(noBiasTheta2 .^ 2)));
J = term1 + term2;

同样可以再次运行ex4，验证结果的正确性。

sigmoidGradient

计算sigmoid函数的梯度，输入可以是向量、矩阵，注意是点乘

sigmoidGradient.m

1
2
3
function g = sigmoidGradient(z)
	g = sigmoid(z).*(1-sigmoid(z));
end

梯度计算

首先实现一个不带正则化的backprop算法。花费我比较多时间的地方大概就是向量化实现了吧。虽然课程中老师说用for循环，而我一开始也打算用for循环实现。但是，首先就发现了delta3可以不用循环就算出来，然后紧接着发现后面的也并不需要循环。需要注意的地方就是矩阵的维数。算得的delta2其实第一列是bias unit的，维数是m*26，然而BigDelta1的维数是25*401，因此要把delta2的有关bias unit那一列去掉。

课程论坛中也提到：如果是用了sigmoidGradient(z2)的化，计算$\delta^{(2)}$时就必须把$\Theta^{(2)}$的第一列去掉；如果是用了$a2.*(1-a2)$的话，计算$\Delta^{(1)}$的时候就要把$\delta^{(2)}$的第一列去掉

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
delta3 = zeros(m,num_labels);
delta2 = zeros(m,hidden_layer_size);

% we have computed a2 and a3(hypothesis) above, they are matrix, one row correspond to one example
% we need to use the extended matrix Y

delta3 = hypothesis - Y;
delta2 = delta3 * Theta2 .* (a2 .* (1-a2));

delta2(:,1) = [];
BigDelta1 = delta2' * X;
BigDelta2 = delta3' * a2;

Theta1_grad = 1/m * BigDelta1;
Theta2_grad = 1/m * BigDelta2;

接下来实现带正则化的backprop算法，注意1/m是在外面的

1
2
Theta1_grad = 1/m * (BigDelta1 + lambda * noBiasTheta1);
Theta2_grad = 1/m * (BigDelta2 + lambda * noBiasTheta2);

最后的unroll代码文件中也有给出。

编程作业5 Regularized Linear Regression and Bias v.s. Variance

此次练习中，实现正则化的线性回归，并用它取研究带有不同bias-variance特征的模型。

Regularized Linear Regression

费用函数和梯度计算

正则化的线性回归的费用函数和梯度计算。和前面实现过的类似。

linearRegCostFunction.m

1
2
3
4
5
6
7
8
9
10
11
12
13
function [J, grad] = linearRegCostFunction(X, y, theta, lambda)
    m = length(y); % number of training examples
    J = 0;
    grad = zeros(size(theta));
    hypothesis = X * theta;
    square_error = sum((hypothesis - y).^2);
    regularized_theta = theta;
    regularized_theta(1) = 0;
    regularized_term = regularized_theta' * regularized_theta;
    J = 1/(2*m) * square_error + lambda/(2*m) * regularized_term;

    grad = 1/m * X' * (hypothesis - y) + lambda/m * regularized_theta;
end

Bias-Variance

Learning Curves

学习曲线，绘制样本大小与训练集费用和交叉验证集误差之间的关系。要注意的一点是，计算训练集误差的时候用的是动态变化的样本大小（即给定训练集的子集），而计算交叉验证集误差的时候用的是整个验证集。调用trainLinearReg函数计算出theta，再调用前面写好的函数计算误差，注意调用函数计算误差的时候传入$\lambda$为0，不需要带上正则化的项。把算得的结果放进两个向量里面。

learningCurve.m

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
function [error_train, error_val] = learningCurve(X, y, Xval, yval, lambda)
    m = size(X, 1);

    error_train = zeros(m, 1);
    error_val   = zeros(m, 1);
    for i = 1 : m,
        training_X = X(1:i,:);
        training_y = y(1:i,:);
        theta = trainLinearReg(training_X,training_y,lambda);
        [J_train, grad_train] = linearRegCostFunction(training_X,training_y,theta,0);
        [J_cv, grad_cv] = linearRegCostFunction(Xval,yval,theta,0);
        error_train(i) = J_train;
    error_val(i) = J_cv;
    end
end

Polynomial Regression

根据前面绘制出来的学习曲线，我们发现，当样本容量变大的时候，训练集和交叉验证集的费用都还比较高，属于underfitting(high bias)。因此，尝试一个更复杂的模型。

实现一个函数，建立X(一维向量) 到其p次幂的映射：X_poly(i,:)=[X(i) X(i)^2 ... X(i)^p]

polyFeatures.m

1
2
3
4
5
6
function [X_poly] = polyFeatures(X, p)
X_poly = zeros(numel(X), p);
    for i = 1 : p,
        X_poly(:,i) = X(:,1).^i;
    end
end

用cross validation set选择$\lambda$值

使用cross validation set来评估$\lambda$值选择的好坏。在选好$\lambda$值之后，我们可以用test set来评估模型的预测能力。调用trainLinearReg函数来进行模型的训练，应尝试这样一系列的$\lambda$值：${0,0.001,0.003,0.01,0.03,0.1,0.3,1,3,10}$

计算随$\lambda$的变化，训练集和交叉验证集的误差。

1
2
3
4
5
6
7
8
9
10
11
12
13
function [lambda_vec, error_train, error_val] = validationCurve(X, y, Xval, yval)
    lambda_vec = [0 0.001 0.003 0.01 0.03 0.1 0.3 1 3 10]';
    error_train = zeros(length(lambda_vec),1);
    error_val = zeros(length(lambda_vec),1)
    for i = 1 : length(lambda_vec),
        lambda = lambda_vec(i);
        theta = trainLinearReg(X,y,lambda);
        [J_train, grad_train] = linearRegCostFunction(X, y, theta, 0);
        [J_cv, grad_cv] = linearRegCostFunction(Xval, yval, theta, 0);
        error_train(i) = J_train;
        error_val(i) = J_cv;
    end
end

编程作业6 Support Vector Machines

Support Vector Machines

已经给定了svmtrain.m，大多数的svm packages都会自动加上$x_0 =1$这一项，因此传递参数的时候不用另外再加了。

开始的时候，尝试不同的C值，看看决策边界是怎样的。

SVM with Gaussian Kernels

要使用SVM找到一个非线性的决策边界，我们需要实现一个Gaussian kernel。

gaussianKernel.m

1
2
3
4
5
6
function sim = gaussianKernel(x1, x2, sigma)
	x1 = x1(:); x2 = x2(:);
	sim = 0;
	distance = x1-x2;
	sim = exp(-(distance'*distance)/(2*sigma^2));
end

有了这个之后，就可以画非线性的决策边界了

Example Dataset 3

我们要为dataset3选择合适的参数C和sigma。使用cross validation set中的数据作为选择参数的依据。我们尝试如下的不同C值和sigma值的组合，每一种组合都进行训练，并计算误差，看那一组参数误差值最小，就选择哪一组参数。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
function [C, sigma] = dataset3Params(X, y, Xval, yval)
	C = 1;
	sigma = 0.3;
	C_vec = [0.01;0.03;0.1;0.3;1;2;10;30];
    sigma_vec = [0.01;0.03;0.1;0.3;1;2;10;30];
    Errors = zeros(length(C_vec),length(sigma_vec));
    for i = 1 : length(C_vec),
        for j = 1 : length(sigma_vec),
            C = C_vec(i);
            sigma = sigma_vec(j);
            model= svmTrain(X, y, C, @(x1, x2) gaussianKernel(x1, x2, sigma)); 
            predictions = svmPredict(model,Xval);
            Errors(i,j) = mean(double(predictions ~= yval));
        end
    end
    value = min(min(Errors));
    [row, col] = find(value == Errors);
    C = C_vec(row(1));
    sigma = sigma_vec(col(1));
    Errors
    row
    col
end

Spam Classification

处理邮件

processEmail.m进行邮件的处理，如全换成小写字母，去掉html标签，将URL换成关键词httpaddr，将邮件地址换成关键词emailaddr，把数字换成关键词number，把美元符号换成dollar，提取单词的主干，把缩进和换行等换成一个空格。

需要我们完成的部分是将邮件中出现的单词映射到给定的单词表的索引上。如下，

1
2
3
4
5
6
7
8
vocabListLength = length(vocabList);
for i = 1 : vocabListLength,
    flag = strcmp(str,vocabList{i});
    if flag == 1,
        word_indices = [word_indices i];
        break;
    end
end

这里我用的是for循环，也许有那种find之类的函数可以一下子找到索引

提取特征

现在我们已经有了一个邮件中的单词索引列表。接下来，我们需要进行邮件特征的提取。用一个n维的向量表示邮件的特征，其中n是单词表的长度。若邮件中出现了索引为i的单词，那么就将特征向量的第i维设置成1，也就是说，这个n维的特征表示的是邮件中哪些单词出现过，哪些单词没出现过。

emailFeatures.m

1
2
3
4
5
function x = emailFeatures(word_indices)
    n = 1899;
    x = zeros(n, 1);
    x(word_indices) = 1;
end

x是列向量，word_indices是行向量，一行代码就可以完成工作了。事实上，只要两个都是一维向量（不论行列，都可以一步完成类似的给多个指定索引赋值的工作）

注意，如果x是矩阵的话，会出现如下效果。它把index中的每一个元素都当成了单个的索引，而不是组合起来进行行列索引的。

编程作业7 K-means Clustering and Principal Component Analysis

第一部分的练习，我们将会实现K-means算法并将其应用到图像压缩中。第二部分的练习，我们将会使用PCA进行分析并找到一个更低维数的向量来表示一张人脸图像。

K-menas Clustering

我们将从2D的数据集开始，以获得对K-means算法的一种直觉感受。进一步地，我们将使用K-means算法进行图像压缩——通过减少颜色的数量，找到那些出现最多次数的颜色的数量。

K-means算法由两部分组成：一是找到离每个点最近的centriod，并对样本点进行标记；二是根据样本点的标记移动中心点。

findClosestCentroid.m

1
2
3
4
5
6
7
8
9
10
11
12
13
function idx = findClosestCentroids(X, centroids)
    K = size(centroids, 1);
    idx = zeros(size(X,1), 1);
    m = size(X,1);
    for i = 1 : m,
        example = X(i,:);
        expand_example = repmat(example,K,1);
        measure =  expand_example - centroids;
        distance = sum(measure .* measure,2);
        [val,index] = min(distance);
        idx(i) = index;
    end
end

这里使用了for循环，遍历每一个样本，计算它们离各个中心点的距离，并根据它们离得最近的中心点的索引进行标记。

computeCentroids.m

1
2
3
4
5
6
7
8
9
10
function centroids = computeCentroids(X, idx, K)
[m n] = size(X);
centroids = zeros(K, n);
for i = 1: K,
    row_index = find(idx == i);
    class_i = X(row_index,:);
    number = size(class_i, 1);
    centroids(i,:) = 1/number * sum(class_i);
end
end

Principal Component Analysis

PCA的实现

pca.m

1
2
3
4
5
6
7
function [U, S] = pca(X)
    [m, n] = size(X);
    U = zeros(n);
    S = zeros(n);
    Sigma = 1/m * X' * X;
    [U,S,V] = svd(Sigma);
end

projectData.m

1
2
3
4
5
function Z = projectData(X, U, K)
    Z = zeros(size(X, 1), K);
    U_reduced = U(:,1:K);
    Z = X * U_reduced;
end

recoverData.m

1
2
3
4
5
function X_rec = recoverData(Z, U, K)
    X_rec = zeros(size(Z, 1), size(U, 1));
    U_reduced = U(:,1:K);
    X_rec = Z * U_reduced';
end

编程作业8 Anomaly Detection and Recommender Systems

Anomaly Detection

在此练习中，我们将要实现一个anomaly detection算法，用于探测在服务器中的异常。

Gaussian Distribution

我们假定，搜集到的样本绝大部分都是正常的，我们用它们来计算一个高斯分布的参数。函数传入一个m行n列的矩阵X，一行代表一个样本，一列表示一个特征，我们需要计算这些特征的$\mu$和$\sigma$值

estimateGaussian.m

1
2
3
4
5
6
7
8
function [mu sigma2] = estimateGaussian(X)
    [m, n] = size(X);
    mu = zeros(n, 1);
    sigma2 = zeros(n, 1);
    mu = 1/m * sum(X)';
    mu_ext = repmat(mu,1,m);
    sigma2 = 1/m * sum((X' - mu_ext).^2,2);
end

选择阈值$\epsilon$

我们用F1 score来评估阈值的选择，在cross validation set上面进行操作。其中y=1代表异常的样本。其中，yval向量表示每个样本是异常还是非异常，pval表示预测结果的可能性，当pval小于$\epsilon$时，就判定样本异常。因此true positive是yval=1且pval < $\epsilon$的样本，false positive是yval = 0且pval<$\epsilon$的样本，false negative是yval = 1且pval > $\epsilon$的样本

selectThreshold.m

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
function [bestEpsilon bestF1] = selectThreshold(yval, pval)
bestEpsilon = 0;
bestF1 = 0;
F1 = 0;
stepsize = (max(pval) - min(pval)) / 1000;
for epsilon = min(pval):stepsize:max(pval)
    predictions = (pval < epsilon);
    true_positive = sum(yval & predictions);
    false_positive = sum(~yval & predictions);
    false_negative = sum(yval & (~predictions));
    precision = true_positive / (true_positive + false_positive);
    recall = true_positive / (true_positive + false_negative);
    F1 = 2*precision*recall / (precision + recall);
    if F1 > bestF1
       bestF1 = F1;
       bestEpsilon = epsilon;
    end
end
end

Recommender System

在这部分练习中，我们将实现collaborative filtering学习算法并将它应用到电影评分上。评分是1-5之间，数据集有943个用户，1682部电影。