密码学笔记2——有限域的构造

实验内容

1. 构造有限域GF(2^127)：不可约多项式为f(x)=x^127+x+1；
2. 给出GF(2^127)上的加法、乘法、平方以及求逆的子程序；
3. 将自己的学号转为二进制字符串，看作有限域中的元素a，计算元素的逆元素以及a^20190911(注：二进制的学号每一位数字用四位二进制比特串表示)

实验算法原理

有限域2^127一共有2^127个元素，可以使用一个127比特的二进制串表示有限域中的每一个元素。使用bitset对这个二进制串进行存储。如bitset<127> my_ele("1011")表示的即是多项式x^3+x^+1

加法

由于多项式每一项的系数都只能取0或1，对于这样的多项式，加法和减法是等价的，即对应位进行异或操作

模运算

不可约多项式为 \(p(x) = x^{127}+x+1\) 因此有 \(x^{127} \equiv x+1 \pmod {p(x)}\) 那么，当n大于127时，有 \(x^{n} = x^{127} \times x^{n-127} =(x+1) \times x^{n-127}\) 因此，对于一需要进行模运算的二进制串，就是将它索引大于等于127的且为1的位，转化成（x+1）*x^(n-127)，也就是将二进制串(00…0011)左移n-127位加到二进制串的低127比特上。进行模运算时，注意从高位模起，这样就能确保比当前模运算位高的位全都已经为0

乘法

记两个操作数分别为被乘数和乘数。两个127bit的二进制串相乘，使用一个254bit的串就可以存储结果。

二进制乘法实际上是一个将被乘数左移，乘上乘数对应位置，然后将加到结果上的一个过程。

开始时记结果为0，因此，遍历乘数的每一位i（从索引0的低位开始），被乘数左移i位，乘上乘数第i位的值（0或1），然后将这个加到结果中即可。

最后，调用模函数对乘法的结果进行求模。

平方

对于二进制串 \(a(x) = \sum_{i=0}^{127}a_ix^i\\ a(x)^2 = \sum_{i=0}^{127}a(x)\times a_i \times x^i\\ a(x)^2 = \sum_{i=0}^{127}a_i \times x^{2i}\) 因此，只需要将原二进制串第i位的值对应到结果的第2i位即可

求逆

使用扩展欧几里得算法求逆，记任意多项式为g，不可约多项式为f，在GF(2^127)中，对于不可约多项式，任意一个多项式和它的最大公约式必定为1

则有 \(gx+fy = gcd(g,f)=1\) 我们可以列出这样的一组式子 \(gx_1+fy_1 = k_1\\ gx_2+fy_2 = k_2\) 在初始条件下，我们令x1=1,y1=0,x2=0,y2=1,k1=g,k2=f

在每一轮比较k2和k2的最大幂次，计算两式的最大幂次差为e，幂次大的式子减去幂次小的式子乘上x^e的结果，更新幂次大的式子的值。每一轮计算的时候都记录下x1和x2的值，最终能够得到k的幂次为0的式子，也就是等号右边为1，那么这时候我们就能够得到g的逆即x的值了。

指数

使用快速幂算法

对于x^e，可以将e写成二进制的形式 \(x^e = x^{a_n2^n+a_{n-1}2^{n-1}+...+a_12^1+a_02^0}\\ = x^{a_n2^n}\times x^{a_{n-1}2^{n-1}}...\times x^{a_02^0}\) 其中ai取值为0或1，指示的是e的二进制串对应位置为0或者为1

那么，我们可以记初始结果为1，检查e的最低位，看是否为1，若为1，则答案就乘上x，在这之后，对x进行平方，再将e右移一位。

bitset<SIZE_N> exponent(bitset<SIZE_N> n, bitset<SIZE_N> e){
    bitset<SIZE_N> res(0);
    res[0] = 1;
    if(!e.any()){
        return res;
    }
    while(e.any()){
        if(e[0]&1){
            res = mul(res,n);
        }
        n = square(n);
        e >>= 1;
    }
    return res;
}

完整代码如下

#include<iostream>
#include<string>
#include<bitset>
#include<ctime>
#include<vector>
#define SIZE_N 127
#define r_str "11" //r = x+1
#define TEST_TIMES 1000
using namespace std;
void print_poly(bitset<SIZE_N> target){
    int first = 1;
    for(int i = SIZE_N-1; i > -1; i--){
        if(first){
            if(target[i]){
                if(i)
                    cout<<"x^"<<i;
                else
                    cout<<target[i];
            first = 0;
            }

        }
        else{
            if(target[i]){
                cout<<"+x^"<<i;
            }
        }
    }
    cout<<endl;
    return;
}
bitset<SIZE_N> add(bitset<SIZE_N> op1, bitset<SIZE_N> op2){
    bitset<SIZE_N> res(0);
    res = op1^op2;
    return res;
}
bitset<SIZE_N> mod(bitset<SIZE_N*2> op1, bitset<SIZE_N> r){
    bitset<SIZE_N> res(0);
    bitset<SIZE_N*2> helper;
    bitset<SIZE_N*2> extend_r(r.to_ulong());
    for(int i = SIZE_N*2-1; i >= SIZE_N; i--){
        if(op1[i]){
            helper = extend_r << (i-SIZE_N);
            op1 ^= helper;
            op1[i] = 0;
        }
    }
    //低位的直接放到结果里面
    for(int i = 0; i < SIZE_N; i++) 
        res[i] = op1[i];
    return res;    
}
bitset<SIZE_N> mul(bitset<SIZE_N> op1, bitset<SIZE_N> op2){
    bitset<SIZE_N*2> raw_res(0);//存储两数相乘的直接结果
    bitset<SIZE_N> res(0);//经过模运算之后的结果
    bitset<SIZE_N> r(r_str);//x+1
    bitset<SIZE_N*2> extend_op1(op1.to_string());//需要对其进行左移，故扩展成原长度的两倍
    for(int i = 0; i < SIZE_N; i++){
        if(op2[i]){
            raw_res ^= (extend_op1<<i);
        }
    }
    res = mod(raw_res,r);
    return res;
}
bitset<SIZE_N> square(bitset<SIZE_N> op){
    bitset<SIZE_N> r(r_str);
    bitset<SIZE_N*2> raw_res(0);
    for(int i = 0; i < SIZE_N; i++){
        raw_res[2*i] = op[i];
    }
    return mod(raw_res,r);
}
int max_exp(bitset<SIZE_N+1> op){
    for(int i = SIZE_N; i > -1; i--){
        if(op[i])
            return i;
    }
    return 0;
}

bitset<SIZE_N> inv(bitset<SIZE_N> op){
    bitset<SIZE_N+1> poly(0);
    poly[0] = 1;
    poly[1] = 1;
    poly[127] = 1;
    bitset<SIZE_N+1> k1(op.to_string());
    bitset<SIZE_N+1> k2(poly.to_string());
    bitset<SIZE_N+1> ktemp;
    bitset<SIZE_N> x1(0);
    bitset<SIZE_N> x2(0);
    bitset<SIZE_N> temp;
    x1[0] = 1;
    int diff_exp;
    while(max_exp(k1)){
        diff_exp = max_exp(k1)-max_exp(k2);
        if(diff_exp < 0){
            diff_exp = -diff_exp;
            ktemp = k1;
            k1 = k2;
            k2 = ktemp;
            temp = x1;
            x1 = x2;
            x2 = temp;
        }
        k1 ^= (k2<<diff_exp);
        x1 ^= (x2<<diff_exp);
    }
    bitset<SIZE_N> r(r_str);
    return x1;
    //return mod(x1,r);
}
bitset<SIZE_N> exponent(bitset<SIZE_N> n, bitset<SIZE_N> e){
    bitset<SIZE_N> res(0);
    res[0] = 1;
    if(!e.any()){
        return res;
    }
    while(e.any()){
        if(e[0]&1){
            res = mul(res,n);
        }
        n = square(n);
        e >>= 1;
    }
    return res;
}
void welcome(){
    cout<<"-==============================以下是可交互操作=============================="<<endl;
    cout<<"请输入您想要进行的操作"<<endl;
    cout<<"1.加法运算"<<endl;
    cout<<"2.乘法运算"<<endl;
    cout<<"3.求逆运算"<<endl;
    cout<<"4.指数运算"<<endl;
    cout<<"输入-1退出"<<endl;
    cout<<"==================================== Hello！==============================-"<<endl;
}
bitset<SIZE_N> ten_to_binary(string s){
    int temp;
    string res = "";
    for(int i = 0; i < s.size();i++){
        temp = s[i]-'0';
        bitset<4> helper(temp);
        res += helper.to_string();
    }
    bitset<SIZE_N> bit_of_res(res);
    return bit_of_res;
}
bitset<SIZE_N> generate_random(){
    bitset<SIZE_N> res;
    srand(time(0));
    for(int i = 0; i < SIZE_N; i++){
        res[i] = rand()%2;
    }
    return res;
}
int main(){
    
    bitset<SIZE_N> result_temp;
    vector<int> notcorrect;
    for(int i = 1; i < 65537;i++){
        bitset<SIZE_N> op1(i);
        result_temp = inv(op1);
        result_temp = mul(result_temp,op1);
        if(result_temp.to_ulong() != 1){
            notcorrect.push_back(i);
        }
    }
    cout<<notcorrect.size()<<endl;
    return 0;

    bitset<SIZE_N> result(0);
    cout<<"======================学号求逆以及指数运算结果如下=========================="<<endl;
    //17340027
    string stu_id = "00010111001101000000000000100111";
    //20190911
    string date = "00100000000110010000100100010001";
    bitset<SIZE_N> student_id(stu_id);
    bitset<SIZE_N> require_date(20190911);
    bitset<SIZE_N+1> poly(0);
    poly[0] = 1;
    poly[1] = 1;
    poly[127] = 1;
    cout<<"学号的逆（The inverse of student id 17340027 is:）"<<endl;
    result = inv(student_id);
    cout<<result<<endl;
    print_poly(result);
    cout<<"学号和日期的指数运算（The result of 17340027^20190911 is:）"<<endl;
    cout<<"（说明：这里计算的指数，学号的每一个十进制位处理成四位二进制，而日期是按照整数转换成对应的二进制处理）"<<endl;
    result = exponent(student_id,require_date);
    cout<<result<<endl;
    print_poly(result);
    cout<<"======================学号求逆以及指数运算结果如上=========================="<<endl;

    cout<<"============================测试计算所需时间=============================="<<endl;
    clock_t start,end;
    bitset<SIZE_N> test1 = generate_random();
    bitset<SIZE_N> test2 = generate_random();
    start = clock();
    for(int i = 0; i < TEST_TIMES; i++){
        mul(test1,test2);
    }
    end = clock();
    cout<<"乘法计算"<<TEST_TIMES<<"次的时间为(单位：毫秒）："<<end-start<<endl;
    cout<<"单次乘法运算的时间为（单位：毫秒）："<<(double)(end-start)/TEST_TIMES<<endl;

    start = clock();
    for(int i = 0; i < TEST_TIMES; i++){
        square(test1);
    }
    end = clock();
    cout<<"平方运算"<<TEST_TIMES<<"次的时间为（单位：毫秒）："<<end-start<<endl;
    cout<<"单次平方运算的时间为（单位：毫秒）："<<(double)(end-start)/TEST_TIMES<<endl;

    start = clock();
    for(int i = 0; i < TEST_TIMES;i++){
        inv(test2);
    }
    end = clock();
    cout<<"求逆运算"<<TEST_TIMES<<"次的时间为（单位：毫秒）："<<end-start<<endl;
    cout<<"单次求逆运算的时间为（单位：毫秒）："<<(double)(end-start)/TEST_TIMES<<endl;
    cout<<"==========================测试计算所需时间完毕============================"<<endl;

    int act;
    welcome();
    cout<<"请输入操作(十进制字符串，运算时将使用4bit表示一位十进制数):"<<endl;
    cout<<"（说明：这里输入的所有十进制数，每一个十进制位处理成四位的二进制，而不是直接当作整数处理）"<<endl;
    cin>>act;
    string op1,op2;
    bitset<SIZE_N> operator1,operator2;
    while(act >0 && act < 5){   
        switch (act)
        {
        case 1:
            cout<<"请输入第一个操作数"<<endl;
            cin>>op1;
            cout<<"请输入第二个操作数"<<endl;
            cin>>op2;
            if(op1.size()*4>127 || op2.size()*4 >127){
                cout<<"输入的数太大，不能超过127比特"<<endl;
                continue;
            }
            operator1 = ten_to_binary(op1);
            operator2 = ten_to_binary(op2);
            result = add(operator1,operator2);
            cout<<"加法结果为："<<endl;
            cout<<result<<endl;
            print_poly(result);
        break;
        case 2:
            cout<<"请输入第一个操作数"<<endl;
            cin>>op1;
            cout<<"请输入第二个操作数"<<endl;
            cin>>op2;
            if(op1.size()*4>127 ||op2.size()*4>127){
                cout<<"输入的数太大，不能超过127比特"<<endl;
                continue;
            }
            operator1 = ten_to_binary(op1);
            operator2 = ten_to_binary(op2);
            result = mul(operator1,operator2);
            cout<<"乘法结果为："<<endl;
            cout<<result<<endl;
            print_poly(result);            
        break;
        case 3:
            cout<<"请输入需要进行求逆的数"<<endl;
            cin>>op1;
            if(op1.size()*4>127){
                cout<<"输入的数太大，不能超过127比特"<<endl;
                continue;
            }
            operator1 = ten_to_binary(op1);
            result = inv(operator1);
            cout<<"求逆结果为："<<endl;
            cout<<result<<endl;
            print_poly(result);
            cout<<"验证求逆正确性："<<endl;
            result = mul(operator1,result);
            cout<<result<<endl;
            print_poly(result);    
        break;
        case 4:
            cout<<"请输入底数"<<endl;
            cin>>op1;
            cout<<"请输入指数"<<endl;
            cin>>op2;
            if(op1.size()*4>127 ||op2.size()*4>127){
                cout<<"输入的数太大，不能超过127比特"<<endl;
                continue;
            }
            operator1 = ten_to_binary(op1);
            operator2 = ten_to_binary(op2);
            result = exponent(operator1,operator2);
            cout<<"指数运算结果为："<<endl;
            cout<<result<<endl;
            print_poly(result);    
        break;
        }
        cout<<"请输入操作(十进制字符串，运算时将使用4bit表示一位十进制数):"<<endl;
        cin>>act;
    }
    cout<<"======================================Bye！========================================"<<endl;

}

运行截图

求学号的逆以及20190911次方的结果如下

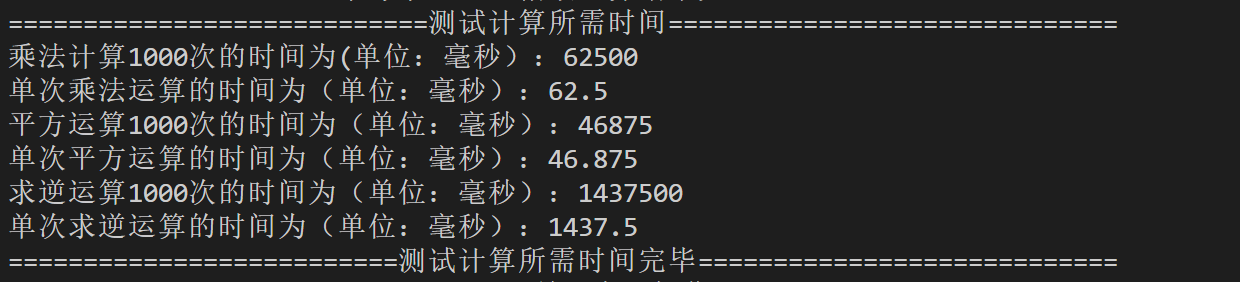
计算乘法、平方、求逆所花费的时间如下：

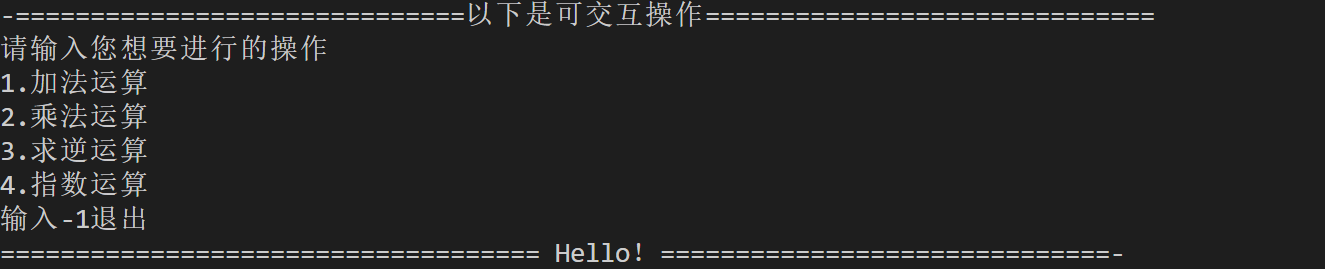
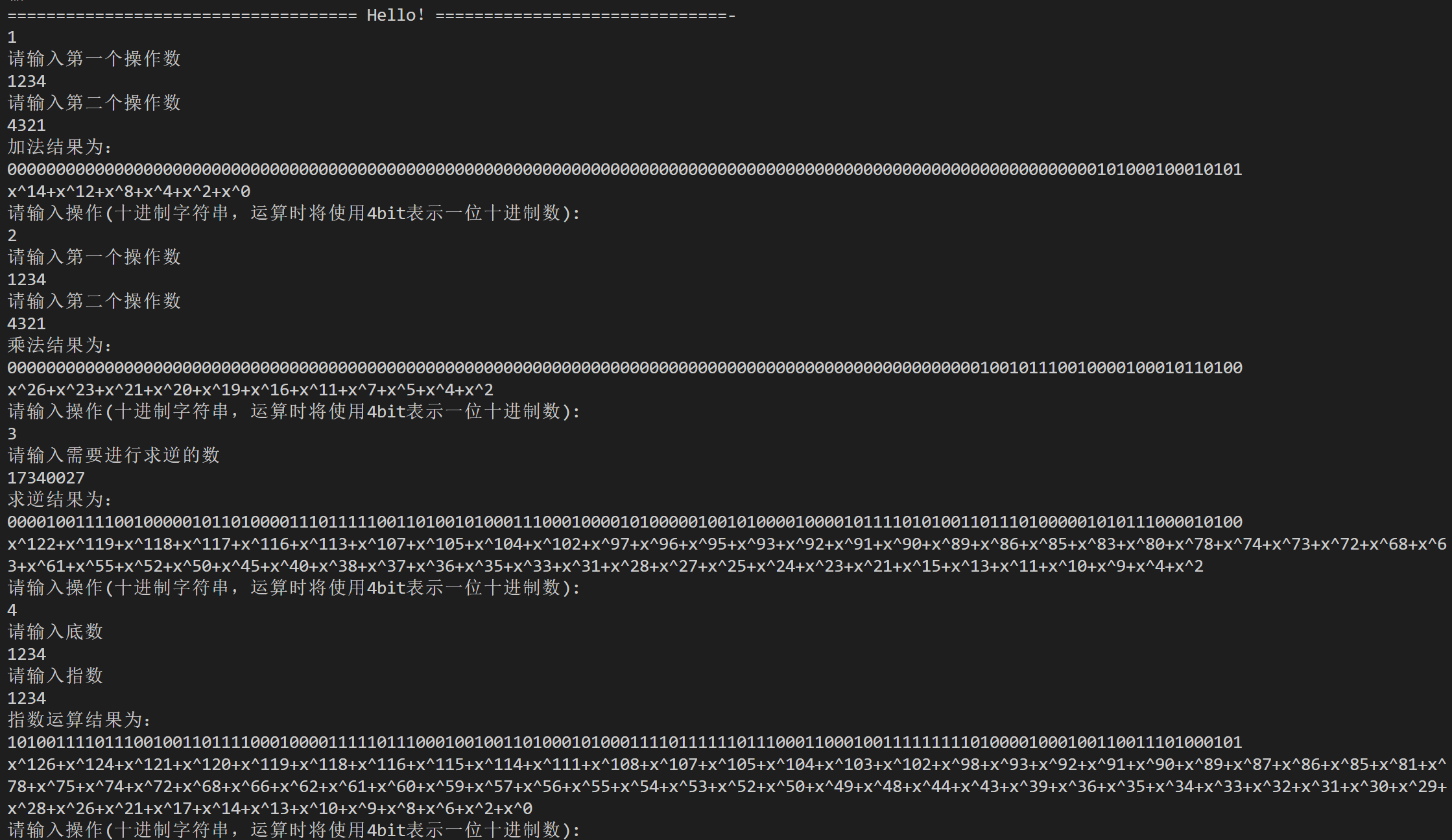
也可以进行交互式加法，乘法，求逆，指数等操作